 |
| ANALIZAR LA FRASE EN CLASE |
Caída Libre
Entre los diversos movimientos que se produce en la naturaleza, siempre ha habido interés en el estudio del movimiento de caída libre de los cuerpos próximos a la superficie de la tierra. Cuando dejamos caer un objeto (Una piedra por ejemplo) desde cierta altura, podemos comprobar que al caer su velocidad aumenta, es decir, su movimiento es acelerado. Si lanzamos un objeto hacia arriba, su velocidad disminuye gradualmente hasta anularse en el punto más alto, osea, el movimiento subida (ascendente) es retardado. Las características de estos movimientos ascendente y descendente son objeto de desde tiempos muy remotos.
Aristóteles y la caída de los cuerpos
Entre los diversos movimientos que se produce en la naturaleza, siempre ha habido interés en el estudio del movimiento de caída libre de los cuerpos próximos a la superficie de la tierra. Cuando dejamos caer un objeto (Una piedra por ejemplo) desde cierta altura, podemos comprobar que al caer su velocidad aumenta, es decir, su movimiento es acelerado. Si lanzamos un objeto hacia arriba, su velocidad disminuye gradualmente hasta anularse en el punto más alto, osea, el movimiento subida (ascendente) es retardado. Las características de estos movimientos ascendente y descendente son objeto de desde tiempos muy remotos.
Aristóteles y la caída de los cuerpos
El gran filósofo griego Aristóteles creía que al dejar caer cuerpos livianos y pesados desde una misma altura, sus tiempos de caída serian diferentes: Los cuerpos más pesados llegarían al suelo antes que los más livianos. La creencia de esta afirmación perduro durante casi 2 milenios, sin que nadie procurase comprobar su veracidad con mediciones cuidadosas.
Esto sucedió en virtud de la gran influencia del pensamiento aristotélico en varias áreas del conocimiento Un estudio mas minucioso del movimiento de la caída de los cuerpos fue realizado por el gran físico Galileo Galilei en el siglo XVII.
Galileo y la caída de los cuerpos
Galileo es considerado el creador del método experimental en física, estableciendo que cualquier afirmación relacionada con algún fenómeno debía estar fundamentada en experimentos y en observaciones cuidadosas. Este método de estudio de los fenómenos de la naturaleza no se había adoptado hasta entonces, por lo cual varias conclusiones de Galileo se oponían al pensamiento de Aristóteles.
Al estudiar la caída de los cuerpos mediante experimentos y mediciones precisas Galileo llego a la conclusión de que si se dejan caer simultáneamente desde una misma altura un cuerpo liviano y otro pesado, ambos caerán con la misma aceleración, llegando al suelo en el mismo instante, contrariamente a lo que pensaba Aristóteles.
Caída libre en el aire y en el vacío
Cuando se deja caer una pluma y una piedra al mismo tiempo y desde una misma altura la piedra cae más deprisa como afirmaba Aristóteles. Pero es posible demostrar que tal cosa sucede porque el aire produce un efecto retardador en la caída de cualquier objeto y que dicho efecto ejerce una mayor influencia sobre el movimiento de la pluma que el de la piedra, si dejamos caer la pluma y la piedra dentro de un tubo del cual se extrae el aire (se crea un vació) comprobamos que ambos objetos caen en forma simultanea como afirma Galileo.
REPRESENTACIÓN GRÁFICA DEL MOVIMIENTO DE CAÍDA LIBRE
RESENTACIÓN GRÁFICA DEL MOVIMIENTO DE LANZAMIENTO DE UN CUERPO
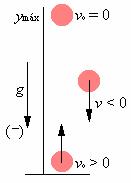
Para el lanzamiento vertical nos encontramos con que  es positiva, y así se mantendrá aún cuando su módulo llegue a valer cero. Esto ocurrirá en el punto más alto de la trayectoria, en el cual la
es positiva, y así se mantendrá aún cuando su módulo llegue a valer cero. Esto ocurrirá en el punto más alto de la trayectoria, en el cual la  , pues pasará de valores positivos a negativos. En ese punto de la altura máxima, el móvil se encontrará parado durante un instante, después del cual comenzará caer. Durante todo el movimiento la aceleración que sufrirá la partícula será la de la gravedad, la cual siempre tiene el mismo sentido, hacia abajo y, por convenio, negativo.
, pues pasará de valores positivos a negativos. En ese punto de la altura máxima, el móvil se encontrará parado durante un instante, después del cual comenzará caer. Durante todo el movimiento la aceleración que sufrirá la partícula será la de la gravedad, la cual siempre tiene el mismo sentido, hacia abajo y, por convenio, negativo.
 es positiva, y así se mantendrá aún cuando su módulo llegue a valer cero. Esto ocurrirá en el punto más alto de la trayectoria, en el cual la
es positiva, y así se mantendrá aún cuando su módulo llegue a valer cero. Esto ocurrirá en el punto más alto de la trayectoria, en el cual la  , pues pasará de valores positivos a negativos. En ese punto de la altura máxima, el móvil se encontrará parado durante un instante, después del cual comenzará caer. Durante todo el movimiento la aceleración que sufrirá la partícula será la de la gravedad, la cual siempre tiene el mismo sentido, hacia abajo y, por convenio, negativo.
, pues pasará de valores positivos a negativos. En ese punto de la altura máxima, el móvil se encontrará parado durante un instante, después del cual comenzará caer. Durante todo el movimiento la aceleración que sufrirá la partícula será la de la gravedad, la cual siempre tiene el mismo sentido, hacia abajo y, por convenio, negativo.

En el vacío el movimiento de caída es de aceleración constante, siendo dicha aceleración la misma para todos los cuerpos, independientemente de cuales sean su forma y su peso.
La presencia de aire frena ese movimiento de caída y la aceleración pasa a depender entonces de la forma del cuerpo. No obstante, para cuerpos aproximadamente esféricos, la influencia del medio sobre el movimiento puede despreciarse y tratarse, en una primera aproximación, como si fuera de caída libre.
La aceleración en los movimientos de caída libre, conocida como aceleración de la gravedad, se representa por la letra g y toma un valor aproximado de 9,81 m/s2 (algunos usan solo el valor 9,8 o redondean en 10).
Si el movimiento considerado es de descenso o de caída, el valor de g resulta positivo como corresponde a una auténtica aceleración. Si, por el contrario, es de ascenso en vertical el valor deg se considera negativo, pues se trata, en tal caso, de un movimiento decelerado.
Para resolver problemas con movimiento de caída libre utilizamos las siguientes fórmulas:
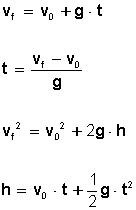
Movimiento de subida o de tiro vertical
Al igual que la caída libre, este es un movimiento uniformemente acelerado.
Tal como la caída libre, es un movimiento sujeto a la aceleración de la gravedad (g), sólo que ahora la aceleración se opone al movimiento inicial del objeto.
A diferencia de la caída libre, que opera solo de bajada, el tiro vertical comprende subida y bajada de los cuerpos u objetos y posee las siguientes características:
- La velocidad inicial siempre es diferente a cero.
- Mientras el objeto sube, el signo de su velocidad (V) es positivo.
- Su velocidad es cero cuando el objeto alcanza su altura máxima.
- Cuando comienza a descender, su velocidad será negativa.
- Si el objeto tarda, por ejemplo, 2 s en alcanzar su altura máxima, tardará 2 s en regresar a la posición original, por lo tanto el tiempo que permaneció en el aire el objeto es 4 s.
- Para la misma posición del lanzamiento la velocidad de subida es igual a la velocidad de bajada.
Para resolver problemas con movimiento de subida o tiro vertical utilizamos las siguientes fórmulas:
Algunos consejos para resolver problemas de caída libre:
Recuerda que cuando se informa que “Un objeto se deja caer” la velocidad inicial será siempre igual a cero (v0 = 0).
En cambio, cuando se informa que “un objeto se lanza” la velocidad inicial será siempre diferente a cero (vo ≠ 0).
VIDEO QUE CAE MÁS RÁPIDO: CAÍDA LIBRE
VIDEO
Galileo Galilei, su vida y descubrimientos
VIDEO SOLUCION DE PROBLEMA DE CAÍDA LIBRE
EXPERIENCIA DE LABORATORIO VIRTUAL SOBRE CAÍDA LIBRE
http://webs.um.es/gregomc/LabESO/CaidaLibrePlanetaria/CaidaLibrePlanetaria.htmlhttp://www.educaplus.org/movi/4_2caidalibre.html mosila-- laboratorio caída libre --masas con diferente gravedad - graficas ---análisis
INSTITUCIÓN
EDUCATIVA TÉCNICA MEDALLA MILAGROSA
CHAPARRAL -
TOLIMA
CINEMÁTICA
DEL MOVIMIENTO RECTILINEO
LABORATORIO
VIRTUAL
DETERMINACION
DE LA ACELERACIÓN DE LA GRAVEDAD DE ALGUNOS PLANETAS
1. OBJETIVOS
1.1 Determinar experimentalmente el valor de la aceleración de la gravedad para algunos planetas del sistema solar
1.2 Utilizar la Ley de interacción Gravitatoria de Newton
1.3 Considerar la caída libre de algunos objetos,
que experimentan un movimiento uniformemente acelerado
1.4 Aplicar las ecuaciones de caída libre
1.5 Conocer algunos elementos del movimiento de
caída libre
1.6 Consultar el fundamento teórico y practico del
movimiento de caída libre
1.7 Resolver problemas mediante talleres
Realiza
una introducción a tu informe.
3. MATERIALES
3.1 Una ventana gráfica con una torre con escala de
alturas
3.2 Objeto
3.3 Menú desplegable de algunos planetas (Tierra,,
Luna, Venus, Marte y Júpiter)
4. FUNDAMENTO
TÉRICO
Relacione
a tu informe: conceptos o definiciones, biografías de científicos que aportaron
avances en el desarrollo histórico del Movimiento de Caída Libre, gráficas, ecuaciones,
sistemas de unidades y ejemplos representativos del tema.
5. PROCEDIMEINTO
DESARROLLO EXPERIMENTAL
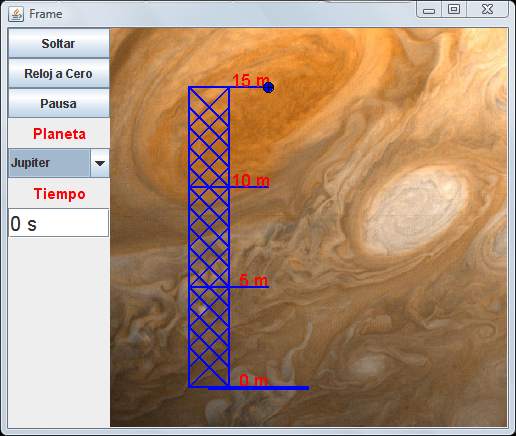
En esta práctica vamos a determinar el valor de la gravedad en distintos planetas del sistema solar. Para ello contamos con una ventana gráfica con una torre desde la que soltaremos un objeto desde tres posible alturas (5m, 10m y 15m), el planeta podemos cambiarlo utilizando el menú desplegable "Planeta"
Selecciona
el planeta a determinar la aceleración de la gravedad
·
Pulsar el botón "Reloj a Cero" para
iniciar el cronómetro.
· Situar con el ratón el objeto en una de las
plataformas de la torre, cuya altura se indica, y pinchar en el botón "Soltar".
·
El objeto empezará a caer y el reloj a contar,
ambos se detendrán automáticamente al llegar al suelo de la plataforma.
· Anotar el tiempo y la altura en las columnas
correspondientes, repetir la experiencia desde otra plataforma. Realizar tres
medidas (para y , t)
·
Aplicar la ecuación de caída libre:
6. DATOS EXPERIMENTALES
Completar las
siguientes tablas, con diferentes
planetas
| PLANETA: TIERRA | |||
| y (m) | t (s) | t2 | g (exp.) |
| PlANETA: LUNA | |||
| y (m) | t (s) | t2 | g (exp) |
| PLANETA: VENUS | |||
| y (m) | t (s) | t2 | g (exp) |
| PLANETA: MARTE | |||
| y (m) | t (s) | t2 | g(exp) |
| PLANETA JUPIT | |||
| y (m) | t (s) | t2 | g (exp) |
Calcular el valor de g como
la media aritmética de los tres valores obtenidos, para cada planeta
g= m/s2
Compara el valor de la gravedad experimental
obtenido con su valor teórico, ver tabla
inferior
| Planeta | g (teor.) | g (exp.) |
| Tierra | 9.8 | |
| Luna | 1.6 | |
| Venus | 9.9 | |
| Marte | 3.7 | |
| Júpiter | 23.1 |
7. CÁLCULOS
Completa las tablas
anteriores, realizando los cálculos pertinentes, mediante procedimientos
algebraicos y aritméticos; utilizando las diferentes ecuaciones
8 ACTIVIDADES
Realiza el taller No 10 de
la Física Investiguemos 10, incluya los enunciados y desarrollo en este punto
9. CONCLUSIONES
Escriba tantas conclusiones como sea posible, de
conformidad con los resultados experimentales y teóricos.
10. BIBLIOGRFÍA
Relacione todas las fuentes bibliográficas
utilizadas
OBSERVACIONES
·
Aplique las técnicas de elaboración de trabajos escritos
·
Entregue el informe en la fecha acordada en clase
·
Evaluación escrita del informe lo sustenta un integrante del grupo
·
Todos los integrantes del grupo deben tomar los datos experimentales
·
El profesor no dará datos ante la perdida de estos
EXPERIENCIA DE LABORATORIO VIRTUAL SOBRE CAÍDA LIBRE
http://www.unefaportuguesa.com.ve/lvf/caidaLibre/index.html
http://perso.wanadoo.es/cpalacio/caidaCuerpos2.htm EXPERIENCIA DE LABORATORIO VIRTUAL SOBRE CAÍDA LIBRE
http://www.juntadeandalucia.es/averroes/ies_sierra_magina/d_fyq/laboratorio%20virtual.htm
¿Cuál llegará antes al suelo?
|
Objetivos
| ||
| Estudiar qué variables están relacionada con la velocidad de caída de los cuerpos |
Parece que los cuerpos más pesados caen más rápidos; las apariencias engañan.
Si dejamos caer una moneda y un trozo de papel de un tamaño similar veremos que la moneda cae antes. ¿Significa esto que como la moneda es más pesada que el papel, los cuerpos pesados caen antes?
Si dejamos caer ahora la moneda y el mismo papel, esta vez hecho una pequeña bola, ¿llegará al suelo antes la moneda? ¿Tendrá algo que ver la forma con la rapidez con la que caen los cuerpos?
EXPERIENCIA
Tenemos varios cuerpos a los que podemos variar su forma, su masa, el medio en el que caen. tmbién podemos ver la gráfica altura/tiempo
EXPERIENCIA DE LABORATORIO VIRTUAL
“Caída libre de los cuerpos”
APRENDIZAJE ESPERADO :
Diferenciar la caída libre de los cuerpos de la caída vertical.
Los siguientes applest de java te permitirán comprender cómo es la caída de los cuerpos en el aire y en el vacío. Puedes cambiar masas, formas, densidades.
CAIDA VERTICAL DE LOS CUERPOS
Observa las gráficas del movimiento. Anota los tiempos. ¿Cuál llegará antes al suelo? ¿El más pesado? ¿Depende de su forma? ¿De su densidad? ¿O todos caen al mismo tiempos?
- Cambia la masa y la forma de los cuerpos y observa su caída. Mantener la densidad constante D = 1 kg/m3
Masa
|
Formas / tiempos
| ||
Esférica
|
Apuntada
|
Plana
| |
1 kg
| |||
2,5 kg
| |||
3 kg
| |||
5 kg
| |||
- Deja caer los cuerpos cambiando de masa , forma y densidad del medio
Densidad
|
Masa
|
Formas / tiempos
| ||
Esférica
|
Apuntada
|
Plana
| ||
1,2 kg/m3
|
1 kg
| |||
1,65 kg/m3
| ||||
2,25 kg/m3
| ||||
2,55 kg/m3
|
2 kg
| |||
2,85 kg/m3
|
1 kg
| |||
3 kg/m3
|
5 kg
| |||
RESPONDE:
1. ¿Qué cuerpos caen más rápido en un medio de igual densidad?
2. ¿De qué depende la caída vertical de los cuerpos?
3. ¿Cómo es la caída de los cuerpos de diferente forma , igual masa en un medio de distinta densidad?
4. Si aumentamos la densidad y la masa de los cuerpos , el tiempo empleado es ( menor – igual – mayor)
5. A mayor densidad , igual masa , el tiempo empleado es ( menor – igual – mayor)
6. Conclusiones:………………………………………………………………………………………………………………
ACTIVIDAD
- Desde la parte alta de un edificio se deja caer una pelota, si tarda 3 segundos en llegar al piso ¿cuál es la altura del edificio? ¿Con qué velocidad impacta contra el piso?
Veamos los datos de que disponemos:
Para conocer la velocidad final (vf), apliquemos la fórmula
Ahora, para conocer la altura (h) del edificio, aplicamos la fórmula:
Respuestas:
La pelota se deja caer desde una altura de 44,15 metros e impacta en el suelo con una velocidad de 29,43 metros por segundo.
2. Se lanza verticalmente hacia arriba una pelota con una velocidad inicial de 30 m/s, calcular:
a) Tiempo que tarda en alcanzar su altura máxima.
b) Altura máxima.
c) Posición y velocidad de la pelota a los 2 s de haberse lanzado.
d) Velocidad y posición de la pelota a los 5 s de haber sido lanzada.
e) Tiempo que la pelota estuvo en el aire desde que se lanza hasta que retorna a tierra.
Veamos los datos que tenemos:
Para conocer el tiempo que demora la pelota en llegar a velocidad cero (altura máxima) utilizamos la fórmula
La pelota llega a la altura máxima a los 3,06 segundos y como el tiempo de bajada es igual al de subida, este se multiplica por dos para conocer el tiempo total que permanece en el aire (6,12 segundos).
Ahora vamos a calcular la altura máxima, la que alcanza cuando su velocidad final llega a cero:
Aplicamos la fórmula
La altura máxima que alcanza la pelota hasta detenerse en el aire es de 45,87 metros (desde allí empieza a caer).
Ahora vamos a calcular la velocidad que tuvo cuando habían transcurrido 2 s:
Aplicamos la fórmula, considerando la velocidad como final a los 2 segundos:
Entonces, la velocidad que llevaba la pelota hacia arriba, a los 2 segundos, fue de 10,38 metros por segundo.
Con este dato, podemos calcular la altura que alcanzó en ese momento (2 segundos).
A los 2 segundos la pelota alcanzó una altura de 40,38 metros.
Veamos ahora qué sucede cuando han transcurrido 5 segundos:
Podemos calcular su velocidad usando la misma fórmula
El que obtengamos -19,05 metros por segundo indica que la pelota va cayendo.
También podemos usar la fórmula de caída libre, ya que al llegar a su altura máxima la pelota tiene cero velocidad, pero a los 5 segundos informados debemos restarle los 3,06 segundos durante los que la pelota ha ascendido hasta su altura máxima y desde donde empieza a caer:
Entonces tenemos
5 s – 3,06 s = 1,94 segundo de caída libre, y su velocidad la dará la fórmula
Pero ahora la velocidad inicial es cero, entonces
Ahora podemos calcular la altura a que ha llegado la pelota a los 5 segundos; o sea, cuando va cayendo y lleva una velocidad de 19,03 metros por segundo:
Transcurridos 5 segundos, la pelota va cayendo y se encuentra a 27, 41 metros de altura.
Una pregunta adicional ¿cuánto ha descendido la pelota desde su altura máxima?
Ya sabemos que la altura máxima fue 45,87 metros, entones a esa altura le restamos los 27,41 metros y resulta que la pelota ha descendido 18,46 metros.
Ejercicio de práctica
Resolvamos ahora el siguiente problema:
Un objeto es eyectado verticalmente y alcanza una altura máxima de 45 m desde el nivel de lanzamiento. Considerando laaceleración de gravedad igual a 10 m/s2 y despreciando efectos debidos al roce con el aire, ¿cuánto tiempo duró el ascenso?
Veamos los datos que tenemos:
Primero necesitamos calcular (conocer) la velocidad inicial (V0), para ello usamos la fórmula
Ahora, para conocer el tiempo que demora el objeto en llegar a velocidad cero (altura máxima = 45 m) utilizamos la fórmula
Respuesta: El objeto demora 3 segundos en llegar a 45 metros de altura máxima.
Para mayor facilidad en la parte operacional,
tome g=10 m / s2. . En otros problemas se
puede trabajar con g=9.8 m / s2 siempre y cuando
el grado de precisión así lo requiera.
1. Una bomba que se deja caer libremente
desde un avión, tarda 10 segundos en dar en el blanco. ¿A qué altura volaba el avión?
2. Qué velocidad alcanza un cuerpo al cabo de 5 segundos de su
caída?
3. Con que velocidad llega un cuerpo al suelo que se deja caer
desde una altura de 80 m?
4. ¿Con qué velocidad se debe lanzar
verticalmente un cuerpo para que alcance una altura de 490 m?
5. Qué tiempo dura en el aire una piedra
que se lanza verticalmente hacia arriba con una velocidad de 24 m / s?
6. Un cuerpo se lanza verticalmente
hacia arriba y alcanza una altura de 100
m. ¿Con qué velocidad se lanzó?
ECUACIONES
DEL M.C.L. Completa la siguiente tabla,
realizando el proceso algebraico aparte para despejar la variable indicada de cada ecuación:



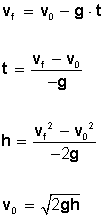
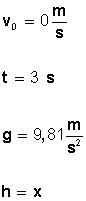
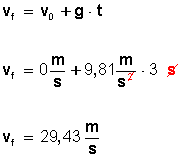
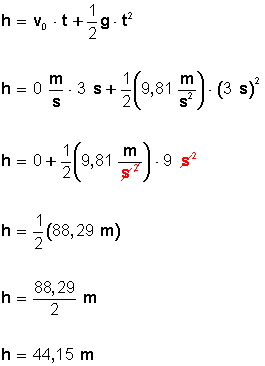
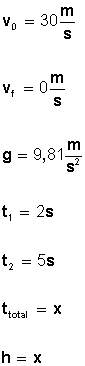
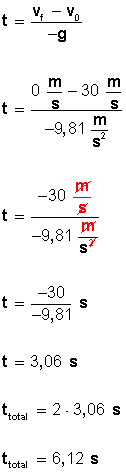
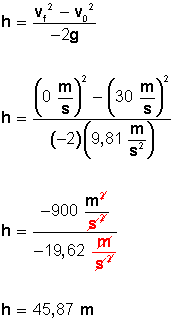
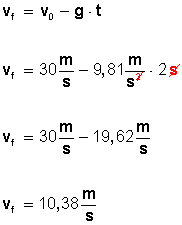
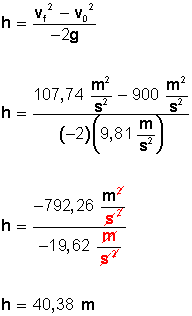
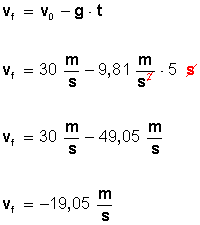
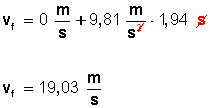
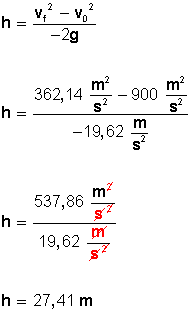
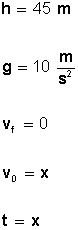
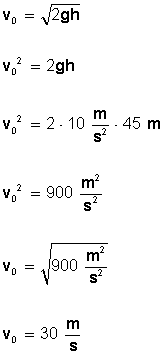
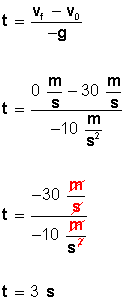
No hay comentarios:
Publicar un comentario